GENERATEURS DE NOMBRES ALEATOIRES

Presque toutes les calculatrices proposent un « générateur de nombres au hasard ». C’est un petit programme qui calcule une suite de nombres pseudo-aléatoires : les nombres sont « uniformément » répartis (c’est le minimum que l’on peut exiger d’eux) le long de l’intervalle [0,1[, mais chacun est, en fait, calculé à partir du précédent. L’utilisateur final ignore la « formule » de calcul utilisée et pour lui les valeurs successives produites semblent tirées au sort. Si votre calculatrice n’a pas de générateur intégré ou pour vous faire une idée, voici un procédé de calcul qui permet d’obtenir des nombres « au hasard ». Choisir un nombre de départ (entre 0 et 1), par exemple zéro virgule le nombre de secondes écoulées depuis 0 heure ce matin ou encore zéro virgule le numéro de série de votre calculatrice ou encore zéro virgule votre date de naissance. Multiplier ce nombre initial par a =147 et ne conserver que la partie décimale du résultat et recommencer avec elle.

Programme RANDOM
h <- donnée (valeur de départ)
Répéter n fois (pour obtenir n nombres au hasard)
h <- FRAC(h) (FRAC est la fonction partie décimale)
Afficher h
Fin répéter

Ce générateur donne des résultats satisfaisants si on examine, par exemple, la fréquence d’apparition des différents chiffres comme premier chiffre après la virgule des nombres engendrés. Voici le résultat d’une expérimentation sur une suite de 1000 nombres.

Pourquoi utiliser a=147 dans ce procédé ? Ne pourrait-on simplifier les calculs en utilisant par exemple le facteur multiplicatif 2, ou 6, ou 5 ? Là encore des simulations vont nous convaincre que certains facteurs multiplicatifs ne donne pas une suite satisfaisante.

Pour a=2 on obtient pour 1000 tirages

En fait, la situation ne se dégrade vraiment qu’a partir d’une cinquantaine d’itérations qui mènent immanquablement vers une partie décimale nulle. Le phénomène semble se confirmer pour toutes les valeurs paires de a.

Le facteur a=5 peut nous paraître suspect en raison de l’utilisation de la base dix et pourtant le résultat d’une simulation sur 1000 itérations donne :

Tout facteur a premier semble donner un générateur satisfaisant du point de vue de la répartition du premier chiffre après la virgule.

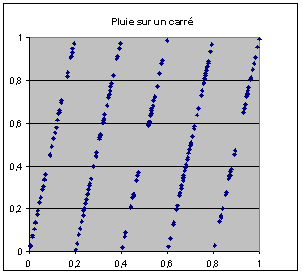
Ces générateurs « affines » ne sont cependant pas utilisables pour toute simulation. Si l’on utilise le facteur a = 5 pour simuler une pluie aléatoire de 200 points sur le carré de côté unité, en choisissant successivement l’abscisse et l’ordonnée du point on observe le phénomène ci-dessous qui s’explique aisément.
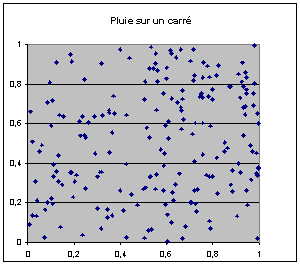
Bien entendu en utilisant pour le tirage de l’abscisse et de l’ordonnée deux valeurs de départ distinctes, c’est à dire deux calculatrices la « pluie » devient plus satisfaisante, mais qu’est-ce donc qu’une pluie aléatoire satisfaisante ?

La définition de ce qu’est un « bon » générateur de nombres aléatoires n’est donc chose aisée, mais il est plus facile de se convaincre qu’un générateur est « mauvais ».
Pour tester le caractère aléatoire d’une suite de nombre l’examen de la fréquence de chaque chiffre ne saurait suffire comme le montre la suite de 30 entiers 0 0 0 1 1 1 2 2 2 3 3 3 4….8 9 9 9 qui n’est guère aléatoire.
Un test plus efficace est inspiré du jeu de poker : on regroupe la suite des chiffres par 5 et on détermine les fréquences de certaines « figures » que l’on compare aux probabilités que l’on sait calculer.

Voici par exemple le résultat du test du poker pour les 2000 premières décimales de p.

(Les décimales de p ont été données par DERIVE et le comptage des figures réalisé avec EXCEL)

Les décimales de p fournissent des chiffres au hasard acceptables. Le test du Chi deux permet de se rassurer sur ce point.

Retour au menu statistique