MATHEMATIQUES A PROPOS
DE LA MARELLE
|
HISTORIQUE
Le nom de marelle (ou mérelles)
viendrait du latin merellus qui signifie pion. Les Grecs jouaient à
diverses variantes de marelle. Ovide décrit ce jeu dans L'Art d'aimer
: "on y joue au moyen de trois pièces pour chaque joueur, sur une
petite table dressée à cet effet ; pour gagner il faut amener
ses trois pièces sur une même ligne".
Sa popularité tient également
au fait que le matériel nécessaire pour jouer est rudimentaire
: quelque lignes tracées dans le sable et des caillous suffisent.
|
|
|
LA REGLE DU JEU
La marelle se joue à deux sur un plateau de 24
points dont certains sont reliés trois par trois en "moulins".
Chaque joueur dispose, au départ, de 9 pions d'une couleur.
La partie se déroule en trois phases successives
:
La pose :
Dans la première phase, les joueurs
posent chacun à son tour l'un de leurs pions sur l'un des points
vides du plateau. Si l'un des joueurs parvient à "fermer" un moulin
en alignant trois de ses jetons, il ôte l'un des pions de son adversaire
choisi parmi ceux qui ne font pas partie d'un moulin fermé.
Les déplacements :
Lorsque les joueurs ont posé tous
leurs jetons, débute la seconde phase du jeu. Les joueurs doivent
à présent pousser l'un de leurs jetons sur un point voisin
auquel le point de départ est relié par un moulin. Le but
reste d'essayer fermer un moulin pour prendre un des pions de l'adversaire
ou de bloquer les pions de l'adversaire qui perd la partie si aucun de
ses pions ne peut bouger.
Les sauts :
Lorsque l'un des joueurs n'a plus que
trois pions, il peut "sauter" c'est à dire déplacer l'un
de ses pions sur l'un quelconque des points libres du jeu. Un joueur qui
n'a plus que deux pions, ou qui ne peut plus se déplacer lorsque
c'est à son tour de jouer a perdu.
|
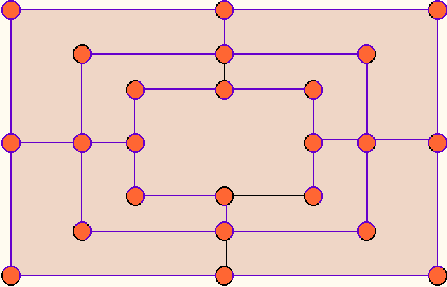
Le plateau de jeu de la marelle habituelle.

Illustration d'un manuscrit du Moyen âge.
|
LE PROBLEME
Le problème que nous allons tenter de résoudre
est celui de l'existence d'autres plateaux de jeu sur lesquels il est possible
de jouer à la marelle en conservant la règle usuelle.
Définition : on appelle
plan de marelle un ensemble de points contenant des sous ensembles appelés
moulins et vérifiant les axiomes suivants :
A1 Chaque moulin contient exactement
3 points (l'essence de la règle du jeu)
A2 Tout point est sur exactement deux
moulins (cela rend les points relativement équivalents stratégiquement).
A3 Par deux points passe au plus un moulin
(laisse au joueur qui joue en second une petite chance de l'emporter)
A4 Il existe une disposition de l'ensemble
des points telle que les moulins soient des segments. (facilite la reconnaissance
des moulins)
A5 Il est toujours possible de relier
deux points en suivant des moulins. (condition de connexité)
Exercices :
a) Vérifier que le jeu "usuel" de marelle
vérifie ces 5 axiomes.
b) Trouver un plan de marelle ayant le moins
possible de points.
Théorème 1 :
Dans un plan de marelle, si p est le
nombre de points et m le nombre de moulins on a :
3m=2p
Théorème 2 :
Pour tout entier n supérieur à
1, il existe un plan de marelle ayant 3n points et 2n moulins.
Théorème 3 :
Les cinq axiomes A1, A2, A3, A4 et A5 sont indépendants
c'est à dire qu'en enlevant l'un quelconque d'entre eux, il existe des
ensembles vérifiant les quatre autres sans vérifier le cinquième.
Les cinq axiomes proposés garantissent
une certaine équité du jeu lors de la première phase (la
pose). Par la suite, il apparaît assez rapidement que certains points
offrent plus de possibilités de déplacements ultérieurs
que d'autres. Dans le plan de marelle usuel, il y a 12 points "doubles" (à
partir desquels on peut aller vers deux autres points s'ils sont libres), 8
points "triples" et 4 points "quadruples". Il n'y a pas de points simples puisque
tout point est sur deux moulins donc relié à au moins deux autres.
Un point est au plus quadruple car il n'est que sur deux moulins (dont il est
le point central s'il est quadruple).
Proposition :
Si on note respectivement p, d, t, q
le nombre de points, de points doubles, de points triples, de points quadruples
et m le nombre de moulins on a :
(1) 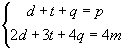
Exercice : dans le cas où p=9,
déterminer tous les triplets d'entiers positifs (d,t,q) solution
du système précédent.
Y a-t-il un plan de marelle correspondant à
chacun des triplets trouvés ?
Solution :
Le système  est équivalent à
est équivalent à 
La seconde équation montre que d
ne peut varier qu'entre 3 et 6 d'où le tableau des solutions :
|
d
|
t
|
q
|
|
3
|
6
|
0
|
|
4
|
4
|
1
|
|
5
|
2
|
2
|
|
6
|
0
|
3
|
Les quatre schémas ci-dessous montrent
qu'il existe effectivement un plan de marelle correspondant à chaque
solution du système :
Théorème 4 :
Pour tout entier n>2 il existe un
plan de marelle à 2n points doubles et n points quadruples
(donc sans points triples).
Démonstration :
|

|
Tracer n rayons de deux cercles concentriques.
On obtient 2n points A1, A2, A3,...,An et B1, B2, B3,...,Bn. On
relie A1B2, A2B1, A2B3, etc.
Les segments se recoupent deux à deux en un point
qui sera quadruple.
Le plan de marelle obtenu aura bien 2n points
doubles et n points quadruples ce qui prouve l'existence d'un tel plan.
|
|

n=6
|

n=4
|
|

n=3
|
Dans le cas n=2, il n'y a pas de
plan de marelle à six points dont 2 quadruples.
|
Théorème 5 :
Pour tout entier n>2 il existe un
plan de marelle à 2n points triples et n points doubles (donc
sans point quadruples).
Démonstration :
|

|
On construit deux polygones réguliers
concentriques de n sommets. On prolonge dans un sens seulement
les côtés du petit qui recoupent les côtés du
grand en des points Ci qui seront les points triples du plan de marelle
obtenu. Par ce procédé, il n'y a aucun point quadruple.
Le dessin ci-contre illustre le cas n=6.
|
Ces deux théorèmes montrent l'existence
pour n>2 des solutions extrêmes car un plan de marelle à
3n points (donc 2n moulins) comporte au plus n points quadruples
(un point quadruple au centre de deux moulins).
Théorème 6 :
Pour tout entier n>2 pair il existe
un plan de marelle avec 3n/2 point doubles, n points triples et
n/2 points quadruples.
Démonstration :
|

|
On représente trois polygones réguliers
concentriques à n/2 sommets. Les côtés et les
médiatrices des côtés forment les moulins.
Les sommets des polygones sont des points
doubles, les milieux des côtés du polygone médian
sont quadruples.
|
Dans le cas où n est pair les trois théorèmes
ci-dessus permettent d'affirmer l'existence des deux solutions extrêmes
et de la solution médiane :
|
d
|
t
|
q
|
|
|
n
|
2n
|
0
|
théorème 5
|
|
...
|
...
|
...
|
|
|
3n/2
|
n
|
n/2
|
théorème 6
|
|
...
|
...
|
...
|
|
|
2n
|
0
|
n
|
théorème 4
|
Théorème 7 :
Dans un plan de marelle comportant au moins
3 points quadruples, il est possible de transformer 2 points quadruples et 2
points doubles en 4 points triples.
Démonstration :
Les deux schémas ci-dessous montrent
comment à partir de la situation en étoile avec beaucoup de points
quadruples, transformer deux points quadruples et deux points doubles en points
triples.
|

Les points doubles A et A' deviennent
les points doubles D et D'.
Les points quadruples B et B' deviennent
triples.
Les points C et C' qui étaient
double de viennent triples.
Sur les nombres de points le bilan est
le suivant :
q ¬ q -
2
t ¬ t +
4
d ¬ d -
2
|

|
Pour n assez grand, il est donc possible,
à partir d'un plan de marelle à n points quadruples de
passer à un plan de marelle à n-2 points quadruples.
Les schémas ci-dessous illustrent le
processus pour n=8 en partant d'un plan de marelle à 24 points
dont 8 sont quadruples.
|

q=8 t=0 d=16
|

q=6 t=4 d=14
|
|

q=4 t=8 d=12
|

q=2 t=12 d=10
|
Les schémas ci-dessous montrent qu'il
est possible d'ajouter 3 points à un plan de marelle en remplaçant
un point quadruple par 2 points quadruples et 2 points doubles (sans changer
le nombre de points triples)
On peut à présent énoncer
le
Théorème 8 :
Pour tout n>1 il existe un plan de
marelle à 3n points dont : 2 points
triples, n-1 points quadruples, 2n-1
points doubles.
Démonstration :
Le plan de marelle minimal (à 6 points)
comporte 2 points triples, 3 point doubles et 1 point quadruple. Le procédé
ci-dessus permet d'ajouter 3 points dont 2 doubles et 1 quadruple à un
plan de marelle comportant au moins un point quadruple. On peut donc engendrer
un plan de marelle de 3n points dont 2 triples. Les seules valeurs possibles
de d et q solution du système (1) sont alors 2n-1
et n-1.
On a finalement la situation suivante concernant
l'existence des plans de marelle correspondant aux solutions du système
(1) :
|
d
|
t
|
q
|
|
|
n
|
2n
|
0
|
théorème 5
|
|
...
|
...
|
...
|
théorème 7
|
|
2n-2
|
4
|
n-2
|
théorème 7
|
|
2n-1
|
2
|
n-1
|
théorème 8
|
|
2n
|
0
|
n
|
théorème 4
|
Le théorème 7 permet de montrer
de proche en proche que tous les nombres de points quadruples entre n
et 0 sont possibles.