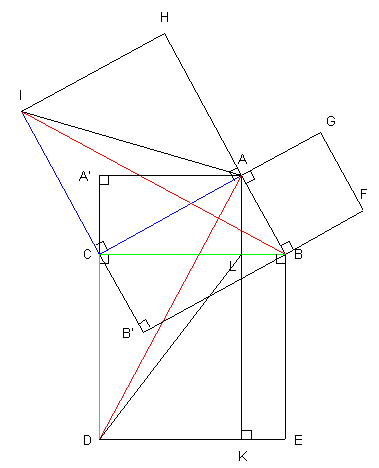Le triangle ABC est rectangle en A. On construit sur ses trois côtés, vers l'extérieur des carrés.

Pour démontrer le théorème de Phytagore, il suffit de montrer que l'aire du plus grand de ces carrés est la somme des aires des deux autres.

La démonstration proposée par Euclide peut se décomposer en trois étapes.

1.. Les triangles ICB et DCA sont isométriques :

D'une part CA=CI et CD=CB et les angles ICB et DCA sont de même mesure.

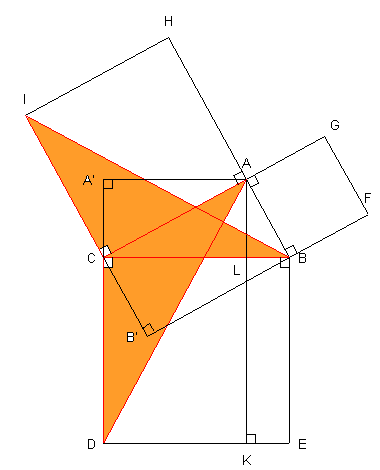2. Les triangles isométriques DCA et ICB ont même aire.

L'aire de ICB est égale à l'aire de ICA (les deux triangles ont la même base [IC] et les hauteurs CA et BB' sont égales).

L'aire de DCA est égale à l'aire de DCL (les deux triangles ont la même base [DC] et les hauteurs CL et AA' sont égales).

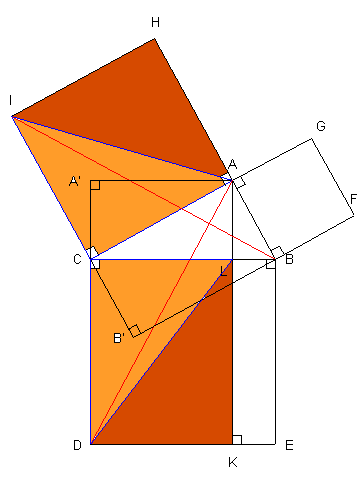3. L'aire du carré ICAH est égale à l'aire du rectangle CLKD (ce sont les doubles des aires des triangles précédents.

Par un raisonnement analogue on prouve que l'aire du carré AGFB est égale à l'aire du rectangle BEKL. Il ne reste plus qu'à additionner.