
En appelant n le plus petit des 4 entiers, la figure ci-contre correspond à un cas, a priori, possible.
En appliquant le théorème de Pythagore successivement aux deux triangles rectangles AHC et AHB, on obtient :
![]()
et
![]()
Trouver tous les triangles dont les longueurs des trois côtés et une hauteur sont 4 entiers consécutifs.
Solution :
|
|
En appelant n le plus petit des 4 entiers, la figure ci-contre correspond à un cas, a priori, possible. En appliquant le théorème de Pythagore successivement aux deux triangles rectangles AHC et AHB, on obtient :
et
|
On en déduit en remplaçant les longueurs par leur expression en fonction de n :

Il reste à écrire que BC = BH + CH ce qui donne :
![]() (1)
(1)
Si n est solution de cette équation (1), il est aussi solution de celle que l’on obtient en élevant les deux membres au carré :

Si n est solution de cette équation (2), il est aussi solution de celle que l’on obtient en élevant les deux membres au carré :

En factorisant et compte tenu du fait que n=0 ne convient pas, on en déduit que s’il y a une solution à notre problème la valeur de n doit être solution de l’équation :
![]()
qui a pour solutions -2 et 12.
Il reste à vérifier que 12 qui est solution de l’équation (4) est bien une solution de l’équation (1) c’est à dire nous fournit un triangle qui convient ce qui n’est plus très difficile.
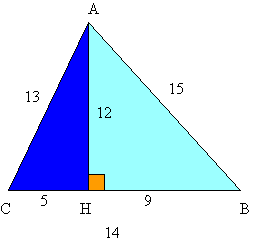
Il y a d’autres cas de figures ( BC = n+1 ou BC = n avec AH = n+1 etc...) qui conduisent à des équations de ce même genre peu sympathique et qui n’ont pas de solution entière. Le triangle trouvé est donc l’unique solution.